Według jednych statystyka to same kłamstwa, a według innych to doskonałe narzędzie do odkrywania i badania prawidłowości zjawisk. Ci pierwsi w tym miejscu mogę przestać już czytać. A pozostałych, którzy nie wierzą w spiskową teorię statystyki, zapraszam do lektury poniższego opracowania.
Jego celem jest zaprezentowanie kluczowych definicji i pojęć ze statystyki opisowej, które po prostu wypada znać, jeżeli ma się cokolwiek wspólnego z pracą na danych lub z badaniami marketingowymi.
Wiele osób miało elementy statystyki na studiach. Niestety z biegiem lat od ich ukończenia powoli zapomina się o pojęciach i wzorach statystycznych. Czas sobie przypomnieć te najważniejsze, które najczęściej przewijają się w opracowaniach badań lub też są najpraktyczniejsze i mogą się okazać bardzo pomocne przy analizie danych.
Gorąco polecam mój podręcznik Excela. Znajdziesz w nim setki przykładów formuł i obliczeń w Excelu, w tym najważniejsze funkcje matematyczne i statystyczne. Nauka Excela to dobra inwestycja. Aby dowiedzieć się więcej o książce elektronicznej Excel – kliknij tutaj -> ’Excel. Nauka na przykładach’
Opisywanie zjawisk za pomocą statystyki
Wzbogacenie analiz o cokolwiek wykraczające poza średnią arytmetyczną sprawia, że zaczyna ona wyglądać bardziej profesjonalnie. Z drugiej jednak strony trzeba wyraźnie zaznaczyć, że nie wszystkie dane nadają się do opisywania statystycznego.
Gdy do marnej jakości danych dodamy nawet najbardziej zaawansowane obliczenia, to na końcu i tak otrzymamy marnej jakości analizę. A gdy do dobrych danych zastosujemy błędne wzory lub metodykę, to także wyjdziemy na podobny wynik jak wcześniej.
Czujność w pracy z danymi jest jak najbardziej wskazana. Statystyka może sprawić, że pewne zjawiska będą bardziej zrozumiałe, ale również nieumiejętne jej użycie może doprowadzić do stanów niepożądanych: zafałszowania rzeczywistości, do powstawania pseudo badań, a przede wszystkim do straty czasu.
Zrozum statystykę i jej cel
Najważniejsze w statystyce jest zrozumienie używanych definicji oraz sposobu wyliczeń, które się za nimi kryją. Obecnie większość wyliczeń można dokonać przy użyciu kilku kliknięć w Excelu, R, SASie i tym podobnych. Ale warto wiedzieć jednak co się tak naprawdę liczy i jak należy interpretować wyniki.
Statystyka to sposób na syntezę danych, której konsekwencją jest jednak utrata pewnych informacji. W zależności od celu badawczego powinny być dobierane odpowiednie narzędzia statystyczne, które pozwolą na znalezienie odpowiedzi na postawione hipotezy.
Na pewno nie jest tak, że im bardziej skomplikowane wzory i metody obliczeń, tym większa poprawność analizy i lepsze wyniki. Często spotykam się z sytuacją wprost odwrotną – im prostsze założenia i krótsze obliczenia, tym bardziej przekonujące rezultaty.
Ktoś, kiedyś powiedział, że jeżeli dane będą torturowane dość długo, wtedy przyznają się do wszystkiego. Bardzo dużo jest prawdy w tym stwierdzeniu. Dla przykładu można przytoczyć badania nad szkodliwością palenia, które były realizowane w ubiegłym wieku przez grono naukowców z tytułami doktora wzwyż.
Jedna strona sporu o zasadność wprowadzenia dodatkowych regulacji ograniczających dostęp do papierosów przedstawiała swoje wyniki badań popierające swoje argumenty. Natomiast druga przy wykorzystaniu tych samych danych dochodziła do zupełnie innych wniosków. Obie strony przy tym były zgodne tylko w jednym, że to ich metodyka analiz jest prawidłowa. Dlatego też należy do wszystkich obliczeń statystycznych podchodzić z odpowiednim dystansem.
Miary statystyczne
Generalnie możemy podzielić miary statystyczne na kilka kategorii. Wyróżniamy następujące rodzaje miar, które w zależności od opracowania mogą przyjmować różne nazwy:
- miary położenia / przeciętne (np.: średnia arytmetyczna, średnia harmoniczna, średnia geometryczna, średnia kwadratowa, kwantyle, moda);
- miary zmienności/ zróżnicowania/ dyspersji (np. wariancja, odchylenie standardowe);
- miary koncentracji (kurtoza);
- miary asymetrii/ skośności.
Średnia arytmetyczna, w skrócie po prostu „średnia”, jest znana praktycznie wszystkim i nie będę się nad nią rozwodził. Przejdźmy od razu do mniej znanych pojęć/
Średnia harmoniczna opisywana jest za pomocą poniższego wzoru.
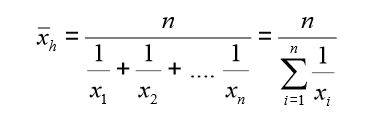
Używana jest ona do uśredniania wartości względnych – czyli przykładowo: prędkości (tj. przebytej drogi do dystansu), udziałów (tj. ilości zbiorowości A, podzielonej przez łączną ilość wszystkich badanych zbiorowości). Zobrazujmy to przykładem: gdy w kolejnych latach udział sprzedaży produktu X w łącznej sprzedaży firmy Z wynosił odpowiednio: 30%, 25%, 20%, wtedy średnia harmoniczna udziału w ciągu 3 lat wynosi = 24% (=3/(3,333+4+5))
Średnia geometryczna to pierwiastek n-tego stopnia z iloczynu liczb (dodatnich). Używa jej się najczęściej do wyliczenia przeciętnego tempa zmian w czasie – np.: gdy dynamika zmian w danym roku względem poprzedniego wynosiła w latach 2010-2013 odpowiednio: 1,1 (tj. wzrost o 10%); 0,9 (tj..spadek o 10%); 0,95; 1,3 wtedy średnia procentowa zmiana w tych latach wynosiła 1,05 (tj. 5%) – tyle właśnie wynosi pierwiastek 4 stopnia z iloczynu wymienionych indeksów – w Excelu średnią geometryczna można wyliczyć przy pomocy funkcji =POTĘGA(ILOCZYN(adres komórek);1/n) – gdzie n to ilość obserwacji, które uśredniamy).

Możemy także się spotkać ze średnią kwadratową, która jest stosowana do obliczania średniej z wartości, które mają różne znaki. Do jej obliczenia korzysta się z następującego wzoru:

Wartości średnie mogą być mocno zniekształcane przez nietypowe obserwacje. Jedna znacząca anomalia w zbiorze danych może zupełnie wypaczyć końcowy wynik. Dlatego, w uzasadnionych przypadkach, przed przystąpieniem do wyliczeń wartości średnich usuwa się określoną ilość obserwacji skrajnych (np. po 10 wartości minimalnych i maksymalnych dla zbioru liczącego 1000 obserwacji) i dopiero po tym dokonuje się wyliczeń.
Najczęstszym błędem popełnianym przy wyliczeniach średniej jest obliczanie jej „ze wszystkiego”. W przypadku, gdy można wyróżnić poszczególne grupy zbiorowości, i po wyliczeniu dla nich średnich okazuje się, że przyjmują one inne wartości, wtedy średnia łączna okazuje się mało istotną informacją.
Warto też pamiętać, że w przypadku, gdy nie dysponujemy całkowitą średnią, a jedynie średnimi cząstkowymi to żeby obliczyć tą pierwszą musimy posłużyć się tzw. średnią ważoną (np. 10 szt. produktu sprzedało się po cenie 5 zł, a 20 szt. po cenie 2 zł, wtedy średnia ważona cena sprzedaży tych 30 szt. wynosi 3 zł ( =(10*5+20*2)/30 = 90/30 ).
Wartości średnie są łatwe w obliczeniach, ale nie dają pełnej charakterystyki struktury zbiorowości – nie jest możliwe przykładowo dowiedzenie się czegokolwiek na temat zmienności badanej cechy. Dlatego wyliczenia warto uzupełniać o dodatkowe pojęcia statystyki opisowej, jak np. następujące.
Dominanta (inaczej mówiąc: modalna, moda lub wartość typowa) to najczęściej występując w danym zbiorze wartość zmiennej. Jest ona bardzo pomocna przy opisywaniu zagadnień ekonomicznych – przykładowo średnia pensja brutto w kraju X wynosi 4 tys., natomiast dominanta wynosi 2,5 tys. – gdyż to jest najczęściej spotykany poziom wynagrodzenia wśród społeczeństwa.
Kwantyle są to wartości zmiennej w badanej zbiorowości, które pod względem liczby jednostek dzielą ją na określone części. I tak wyróżniamy:
- kwartyle – dzielące zbiorowość na cztery części;
- decyle – dzielące zbiorowość na dziesięć części;
- percentyle – dzielące zbiorowość na sto części.
Najczęściej posługujemy się kwartylami, np. przy segmentacji klientów przypisujemy każdego z nich do jednego z 4 kwartyli. Możemy wyróżnić: kwartyl pierwszy (dolny), drugi (tzw. mediana lub kwartyl środkowy) oraz trzeci (górny). Każdy z kwartyli dzieli zbiorowość na dwie części pod względem liczebności, i tak:
- pierwszy kwartyl – dzieli posortowaną zbiorowość w taki sposób, że 25% jednostek ma wartości cechy niższe, a 75% wyższe od kwartyla pierwszego;
- drugi kwartyl – 50% jednostek ma wartości cechy niższe a 50% wyższe od mediany;
- trzeci kwartyl – 75% jednostek ma wartości cechy niższe a 25% wyższe od kwartyla trzeciego.
Jak widać mediana to szczególny przypadek wspomnianych powyżej kwantyli. Mediana dzieli zbiór obserwacji na dwie równe pod względem liczebności części. Z tego bezpośrednio wynika, że jej wartość jest w dużym stopniu uzależniona od ilości przyjmowanych wartości przez zmienną. Z drugiej strony jest ona „odporna’ na występowanie skrajnych, tj. wyjątkowo dużych lub małych, wartości. Ponadto w przypadku rozkładów asymetrycznych (opisanych na rysunku poniżej) pokazuje wartość typową lepiej niż średnia.
Rozstęp (zakres zmienności) to różnica między najwyższą i najniższą wartością zmiennej (MAX – MIN). Przydatna, gdy porównujemy pewne zjawiska w czasie lub porównujemy 2 zbiorowości między sobą. Ale z samej definicji możemy zauważyć, że ten parametr jest bardzo wrażliwy na skrajne wartości
Wariancja określa rozproszenie wartości obserwacji wokół średniej – im wyższa, tym więcej obserwacji jest oddalonych od średniej. Wariancja to podstawowa miara zmienności. Jest opisywana przez wzór na średnią arytmetyczną z kwadratów odległości od średniej.

Odchylenie standardowe opisuje, o ile obserwacje danej zbiorowości różnią się średnio od wartości średniej. Im większa wartość odchylenia standardowego tym obserwacje są mniej skupione wokół średniej. Wzór na odchylenie standardowe to po prostu pierwiastek z wariancji. Odchylenie standardowe wykorzystuje się do konstrukcji typowego obszaru zmienności badanej cechy, dolny i górny zakres tego obszaru wylicza się odpowiednio w następujący sposób: średnia minus odchylenie standardowe, średnia plus odchylenie standardowe).
Współczynnik zmienności jest ilorazem odchylenia standardowego przez średnią arytmetyczną, wyrażany jest zwykle w procentach. Można się spotkać także z innymi wzorami, ale ten przytoczony jest najczęściej stosowany. Współczynniki zmienności opisuje skalę zróżnicowania danych, a jego duże wartości procentowe wskazują na dużą niejednorodność zbiorowości. Współczynnik ten porównuje się między zbiorowościami lub śledzi w czasie.
Kurtoza opisuje rozkład zmiennej, a mówiąc dokładniej stopień jej koncentracji wokół wartości średniej. Służy do oceny tego, w jakim stopniu wszystkie obserwacje są zbliżone do wartości średniej. Im więcej obserwacji jest zbliżonych do wartości średniej wtedy kurtoza przyjmuje wartości powyżej 0, w innym przypadku poniżej 0. Szczegóły na rysunku.
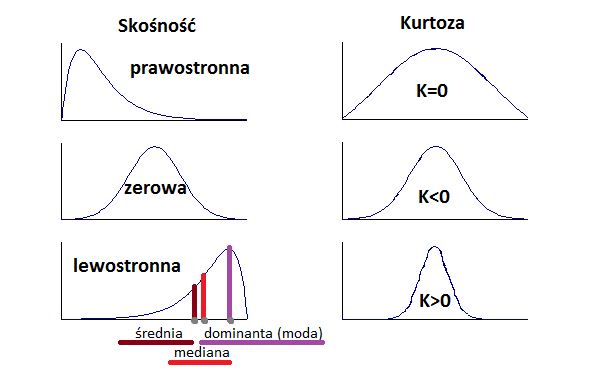
Skośność wskazuje, czy większość obserwacji jest poniżej średniej czy powyżej średniej. W przypadku, gdy więcej jest obserwacji po lewej stronie od średniej (rozkład jest wyższy po lewej stronie), wtedy rozkład jest prawoskośny, tj. występuje asymetria prawostronna; w odwrotnym przypadku, gdy większość obserwacji ma wartość wyższą niż średnia to mamy do czynienia z rozkładem lewo skośnym, występuje asymetria lewostronna.
Korelacja opisuje związki i prawidłowości pomiędzy zmiennymi. Istnieje szereg różnych wzorów, które się wykorzystuje do jej obliczenia (korelacja Spearmana, Kendala, Pearsona, itd.). Ale zazwyczaj większość wyników obliczeń wskaźnika korelacji przyjmuje wartości od -1 do 1.
- Wartość „ -1” oznacza idealnie ujemną prawidłowość (praktycznie nieobserwowana w przyrodzie), czyli że wraz ze wzrostem jednej zmiennej spadają wartości drugiej.
- Wartość „+1” (tak samo trudna do spotkania) oznacza dodani związek, wraz ze wzrostem jednej zmiennej druga wzrasta w analogicznym stopniu.
- Korelacja na poziomie oscylującym wokół 0 oznacza brak związku pomiędzy zmiennymi. Zatem interpretacja wskaźnika korelacji polega na określeniu: kierunku zależności oraz jej siły. Korelacje o wartości do 0,3 traktowane są zwykle jako słabe, te pomiędzy 0,3 a 0,7 jako średnie, natomiast te powyżej 0,7 za silne. Ale te przedziały są czysto umowne, w niektórych przypadkach korelacja na poziomie 0,8 może być traktowana jako słaba, a dopiero ta na poziomie 0,95 jako silna.
Warto zaznaczyć, że mierzenie korelacji nie jest mierzeniem zależności między zmiennymi. W literaturze anglojęzycznej funkcjonuje nawet popularne stwierdzenie „correlation does not imply causation”. Oznacza ono mniej więcej tyle, że wyliczenia mogą wskazywać korelacje pomiędzy zmiennymi, natomiast zdrowy rozsądek powinien nam podpowiadać, że tak naprawdę nie ma żadnej zależności przyczynowej między zmiennymi i żadna z nich w żaden sposób nie wpływa na drugą.
Inne syntetyczne sposoby opisu danych
Do opisu statystycznego nie potrzebne są koniecznie wzory i skomplikowane wyliczenia. Wielu informacji mogą dostarczyć nam wyłącznie wykresy. W jednym z wcześniejszych wpisów opisem i podałem przykłady wizualizacji danych. Wykresy są o wiele bardziej czytelniejsze, a także pozwalają szybciej wychwycić miejsca, na które powinno się zwrócić szczególną uwagę podczas dogłębnych analiz (np. na anomalie). Umiejętność tworzenia histogramu w Excelu okazuje się tutaj bardzo przydatna. Dzięki niemu możemy bardzo szybko opisać rozkład zmiennej.
Bardzo wartościowym i praktycznym sposobem na wzbogacenie statystyki opisowej jest wykorzystywanie analizy wskaźnikowej. Istotę wiele problemów badawczych można ograniczyć do śledzenia zachowania kluczowych wskaźników – ich zmienności w czasie oraz różnic w wartościach pomiędzy innymi zbiorowościami. Na gruncie biznesowym funkcjonują tzw. KPI (key performance indicators) – analogiczne wskaźniki mogą być tworzone do analizy zjawisk i zachowań marketingowych. Mogą być one wykorzystywane do oceny:
- udziałów;
- sezonowości;
- dynamiki, itd.
Jeżeli chcesz poznać praktyczne przykłady obliczeń statystycznych w Excelu, to odsyłam do mojego opracowania – jest to taki Excel podręcznik, który został stworzony z myślą o ułatwieniu nauki korzystania z arkuszy kalkulacyjnych. Jego tytuł to 'Excel. Nauka na przykładach’.
Czeka EXTRA rabat z kodem "10PROC"...
Korzystasz z EXCEL lub PowerPoint?
Poznaj setki praktycznych przykładów!
500 funkcji Excel + 500 slajdów PowerPoint





Dzieki za dobry wpis. Bardzo praktyczna wiedza.